The Two Generals Problem
Table of Contents
Alice and Bob
Imagine there’s a city in a valley. On either side of the valley, there’s an army commanded by a general. On the left hill stands General Alice and her army. On the right hill, General Bob and his army. Alice and Bob want to capture the city, but neither side has an army large enough to do so alone. Both Alice and Bob must attack the city at the same time to have a chance at taking it.
Here’s where we get to the problem. Alice and Bob can only communicate by sending messengers through the valley. These messengers have a chance of being captured by the city’s army. Given this situation, and the condition that Alice and Bob will only attack if they are confident the other will attack at the same time, how do Alice and Bob coordinate their attack?
Let’s say Alice decides to take the initiative. She sends a message to Bob that reads:
“Let’s attack on May 17th. Send a messenger back with your reply. -Alice”
If the messenger doesn’t make it through, Alice won’t attack, and neither, obviously, will Bob. If the message reaches Bob, he’ll send his response:
“OK, let’s do it. May 17th it is! -Bob”
Now here’s the interesting part–it doesn’t matter whether Bob’s reply makes it back or not. Either way, Bob won’t attack. Remember that Bob will only attack if he’s confident Alice will too. Bob knows that Alice will only attack if she gets his reply, but Bob has no way of knowing whether his reply made it back to Alice. If it didn’t, she won’t attack, and if he attacks without her, his army gets wiped out. Since Bob doesn’t know whether his message made it back, he waits and does nothing.
Is there anything we can do? Let’s change it so that Bob asks Alice to send confirmation that she got his reply. Instead of his original reply he sends this:
“OK, let’s do it. May 17th it is! Send another messenger back to confirm that you got this message. -Bob”
So now Alice sends the message, Bob sends his reply, and Alice gets ready to send the acknowledgment message that she received his reply. But she realizes that she has no way of knowing whether he will get the acknowledgment. If he doesn’t get it, he won’t attack, and her army will be defeated. So she decides to send this message:
“I acknowledge your reply. Please send yet another messenger to acknowledge this acknowledgment. -Alice”
To summarize, now we have a message, a reply, an acknowledgment of the reply, and an acknowledgment of the acknowledgment.
Let’s say Bob receives the acknowledgment and prepares to send the acknowledgment of the acknowledgment. But wait! He realizes that he has no way to know whether Alice will get the acknowledgment acknowledgment. If she doesn’t get it she won’t attack, so Bob decides to send:
“I acknowledge your acknowledgment. Please send yet another messenger to acknowledge this acknowledgment acknowledgment. -Bob”
See what’s going on here? It doesn’t matter how many levels of acknowledgment we add, the last person to send a messenger can never know if that messenger got through. Therefore, the last person to send a messenger can never be confident that the other person will attack and so will never attack themselves.
Relaxed Two Generals
The problem above is called the Two Generals Problem, and it’s provably unsolvable. Is there a relaxed version of the problem with fewer constraints that is solvable? Since I probably wouldn’t ask this question if the answer were no–it turns out that yes, there is. If we remove the condition that both generals must be 100% confident that the other one will attack and if we change around a few other things, we can solve the problem most of the time. We still can’t completely guarantee both generals will attack, but we can be reasonably certain they will.
In the new version of the problem, Alice is the leader. She decides when to attack, and once she decides when to attack, she will attack no matter what. If Bob gets a message saying he should attack at a specific time, he must do so. Let’s see an example.
Alice decides that she wants to attack. She knows that she can never be 100% certain Bob will attack as well, but she decides she wants to be 99% certain that he will. Alice knows the length of time it takes a messenger to cross the valley, and she knows the likelihood that the messenger will get caught.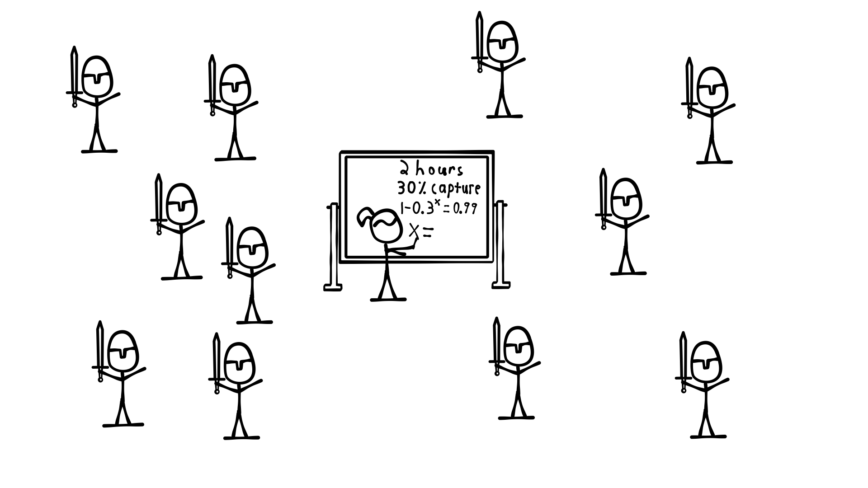
Knowing those two things, she calculates the number of messengers it will take to be 99% certain that one gets through. She then calculates how long it will take to send that many messengers and sets the attack time far enough in the future to allow for this.
Next Alice sends a messenger with the following message:
“Attack next Thursday at 9am. Send a messenger back to acknowledge you received this message.”
Alice then waits enough time for the messenger to get to Bob and for Bob’s acknowledgment messenger to get to her. If the messenger arrives, Alice stops sending messengers, and both Alice and Bob wait around until their coordinated attack next Thursday at 9am.
If the acknowledgment message never arrives, Alice sends another messenger with the same message:
“Attack next Thursday at 9am. Send a messenger back to acknowledge you received this message.”
She keeps repeating the process until either an acknowledgment arrives or it’s next Thursday at 9am, at which time she will attack regardless of whether the message made it through. Because Alice picked a time far enough in the future (based on the failure rate of the messages), there’s a 99% chance that at least one messenger makes it through to Bob before the attack time.
We know there’s a 99% chance both generals attack next Thursday at 9am. Can we increase this certainty number? Yes, we can. Alice can get the number as close to 100% as she wants by setting the attack time further and further into the future. However, she can never get to 100% without setting the attack time infinitely far into the future (which means it will never happen, so that would be useless).
There’s one more thing to point out here. If we didn’t care whether the attacks happened together, Alice could send a message that said:
“Attack now. Send a messenger to acknowledge you received this message.”

In this situation, Alice could keep sending the message over and over again, until she receives an acknowledgment and wait for the acknowledgment before she attacks.
This method does guarantee that both sides will eventually attack, but critically, they won’t attack at the same time. Alice will attack later than Bob by at least the amount of time it takes the acknowledgment messenger to get from Bob to Alice, and possibly much later than that depending on how many messengers are captured.
A more practical example
Let’s take a look at a more practical example. Suppose you are designing a system that needs to book a flight with a 3rd party service and send your user an email that the flight has been booked.
At first it sounds like an easy problem. Make a network call to the flight booking system. If it returns an OK status, then send the email. If it returns an error status, don’t send the email (or send an email that says try again later).
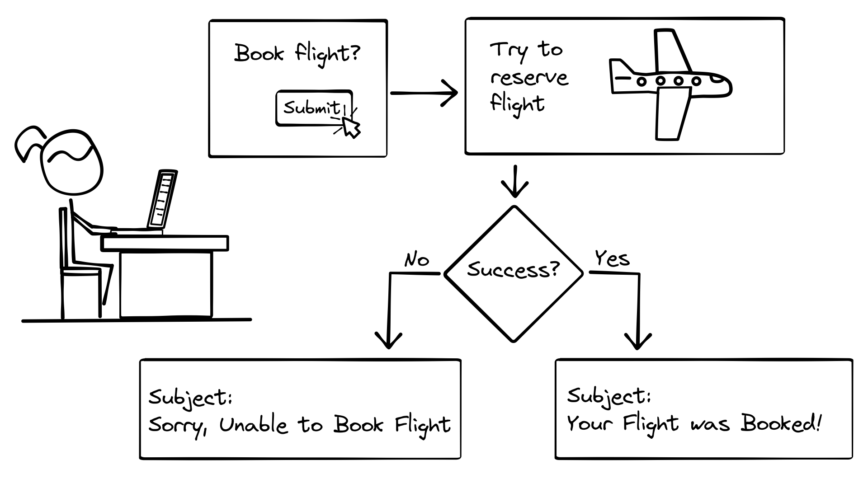
But remember that network calls are unreliable, so what we actually have is a version of the relaxed Two Generals Problem above. If the network call returns an OK or an error status, then we’re fine, but a network call can also timeout because no response was received (just like a messenger being captured). What do we do in that case?
Just like in the relaxed Two Generals Problem, we can keep retrying the messages until we get a response back. Only once we have a response do we decide what to do next. If the response is OK, we send the email (we’re intentionally ignoring that sending an email is also an unreliable operation). If the response is an error, we don’t.
Do you see any problems with this approach? What if something is wrong with the network and we never get a response? Do we just keep retrying forever, potentially blocking resources until someone notices an issue and manually kills the task?
We can deal with this using part of our original solution to the relaxed Two Generals Problem. We’ll add a timer. Specifically, we can add a timeout to our retry process. The first time we send the message to book the flight, we’ll start the timer. Then we’ll keep retrying the message over and over (as long as we don’t get a response) until the timer counts down to zero. Once the timer is done, we’ll stop sending messages and take action.
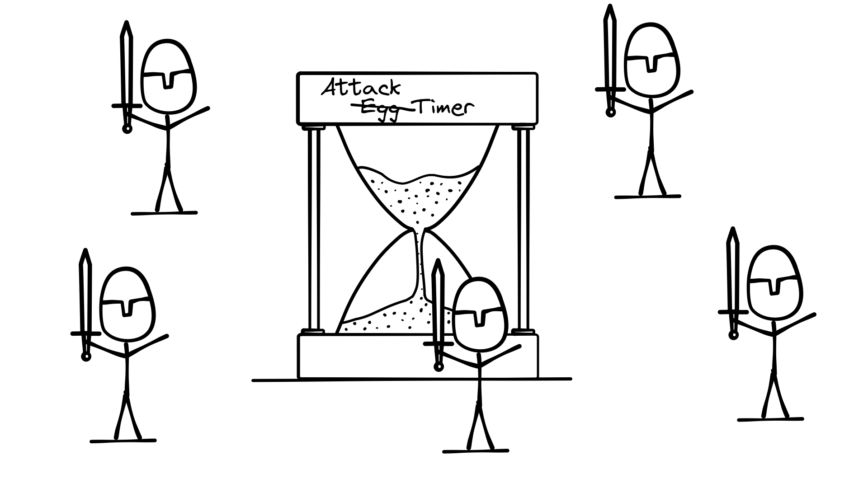
The length of the timer is equivalent to declaring the attack time in the messages to Bob. If we start sending messages at 9am on Wednesday, and Alice decides to attack at 9am on Thursday, we have a 24 hour timeout timer. And just like setting the attack time, we can increase the chances of a message getting through by increasing the length of the timeout. However, we have to balance this by not allowing our system to hog resources for too long.
We know that after the timeout we take action, but we haven’t said what that action is yet. Since we never got a response, we don’t know whether the flight was booked or not. We can either send an email saying it has been booked, send one saying it may have been booked, or send nothing at all (and log a timeout error). The best decision is situational, but in our case we’ll choose to send an email saying the flight may have been booked. The user can then follow up.
For our solution to work, we have to handle another complication, which is a direct consequence of the issues raised by The Two Generals Problem–exactly once message delivery is impossible over an unreliable network. We can send a message once, and hope that it arrives (but it might not), or we can send a message many times. In that case it may arrive more than once (maybe many more times).
Imagine that a messenger gets lost on the way to Bob. Another messenger is then dispatched and reaches the destination directly. After the second messenger has arrived, the first messenger manages to find their way to Bob. The same kind of thing can happen with a computer network. Instead of getting lost, messages can get stuck in buffers along the way.
In the case of our flight booking system, this could be a big problem. If multiple messages arrive saying to book a flight, the system might book multiple flights. To solve this, the book flight request must be idempotent. Idempotent means that if a request is made more than once, the effect of the request must occur only once.
There are a few ways the book flight request can be made idempotent. One way is to include a unique ID with the request. As long as our system sends the same ID on every retry, the flight system can store the ID and use it to ignore all but the first message it gets.
Adding a second distributed operation
So far it seems like we’ve solved all of our problems. However, our system breaks down if we add a second distributed operation. What happens when we want our system to also handle booking hotels? The new requirements are that we should book a flight and a hotel together. That is, we should only book the hotel if the flight is successfully booked, and only book the flight if the hotel is successfully booked. After we book them both, we send an email with a status update.
Even ignoring timeouts, the requirement that both be booked or neither be booked adds complexity. We can handle this complexity in a few different ways, but the most direct is to make sure our system can handle undoing either operation. The approach is known as a Distributed Saga.
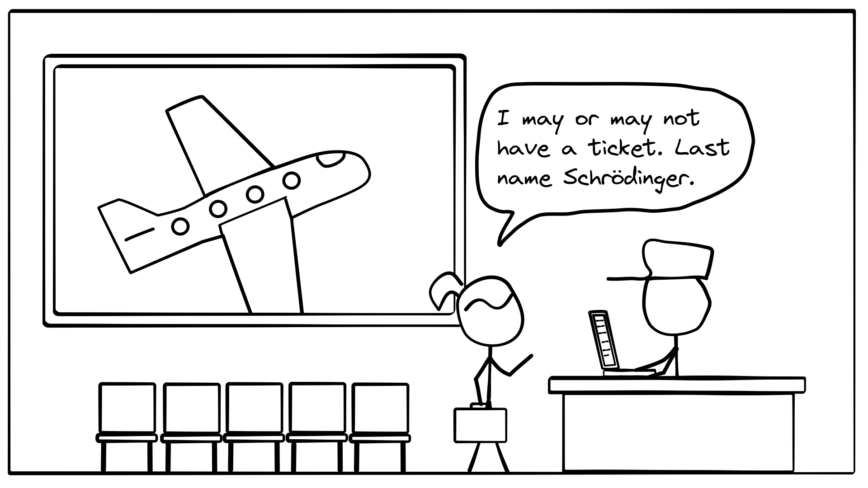
Here’s what a Distributed Saga for our flight and hotel booking system looks like (ignoring timeouts and lost messages): First we send a message to book the flight. If we get an error response, we abort the entire process. If the flight booking system returns a success, we send a message to book the hotel. If that succeeds, we’re done, and we can send the success email.
If, however, the hotel system returns an error, we have to undo the flight booking by calling the flight system with a message telling it to undo the flight we just booked. This is called rolling back the saga. After we roll back the saga, we can send an appropriate message or log an error.
Here’s what that looks like in pseudocode:
We can’t actually ignore lost messages in our real implementation. How do we handle that possibility in our saga? Each distributed action (booking a flight and booking a hotel) must have a corresponding compensating action (canceling a flight reservation and canceling a hotel reservation).
Since we already have them, we can use compensating actions to handle lost messages when calling the original actions. For example:
We start the saga and send a message to book a flight. If the book flight network call times out, instead of retrying we can roll back the entire saga. We call the cancel flight reservation endpoint with the ID we sent along with the original book flight request.
Dealing with timeouts and lost messages
You may have noticed a problem. We don’t know whether the book flight request made it through or not. What if it didn’t and we still send the cancel flight reservation request? In the same way that the book flight request must be idempotent, the combination of book flight and cancel flight reservation must be commutative. The order that the flight reservation system receives them in shouldn’t matter.
If the cancel flight reservation message gets there first, the flight reservation system must store the request ID and block any book flight requests that come in with that ID later. If the cancel flight reservation message gets there after the book flight message, the flight reservation system must undo the original action.
We’ve handled lost messages for the book flight action by kicking the problem over to the compensation action, but what happens if the compensation action request gets lost?
Compensating actions must not be capable of failure. They can never return an error code. That means that the only way they can fail is to timeout. Because of this, we can keep retrying the compensating action until it is successful (in practice, we probably want a timeout here to give up and eventually alert a human that something is wrong).
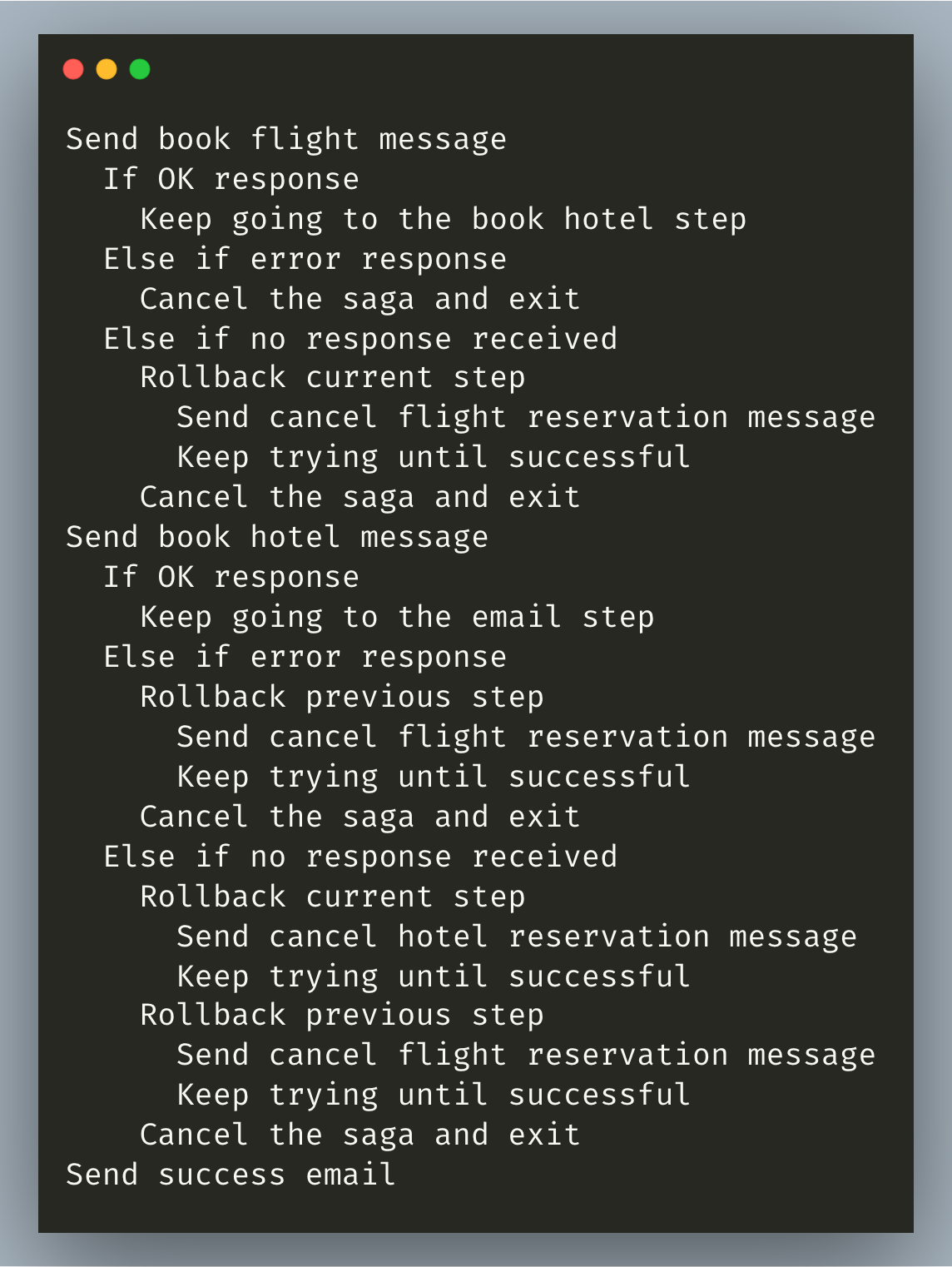
If book flight is successful, we move on to book hotel. If that fails, we rollback the previous step. If it times out, we rollback the current step by calling cancel hotel reservation, then we rollback the previous step, cancel the saga and exit. If everything succeeds, we move on to send the email.
In pseudocode, our final saga looks like this:
Notes for production systems
There are a few final notes worth mentioning for production systems. We’ve dealt with failures of the remote systems, but not with failure of our local system. We also need to store where we are in the current saga so that we can recover from that point in case our system crashes in the middle of it.
Additionally, most of the literature you’ll read about Distributed Sagas will refer to the commutative property as I just did, but commutative isn’t really strong enough to describe what’s required.
Let’s take the simple example of an action within a saga called Increment and its compensating action called Decrement. Unsurprisingly, Increment increments a number by 1, and Decrement decrements it by 1. Together those actions are commutative. Starting from the counter at 0, Increment then Decrement = Decrement then Increment = 0.
0 + 1 - 1 = 0 - 1 + 1 = 0
The final result is the same no matter the order. But a compensating action in a saga must also work when only the compensating action message reaches its destination.
That is, starting from 0, Increment then Decrement = Decrement then Increment = just Decrement = 0.
Instead of saying the action and its compensating action must be commutative, I’ve started referring to this requirement by saying that the compensating action must dominate the action. Increment and Decrement must both be idempotent as well, so no matter how many messages arrive (with the same ID), as long as one Decrement gets there, the final result must be the same as it was before the saga began.
Another example starting at 0:
Increment -> Decrement -> Increment = 0 = Decrement -> Increment -> Decrement
Because of these properties, Decrement isn’t a good name for the compensating action. Better to call it something like Compensate Increment.
One way to implement this is for Compensate Increment to share its ID with Increment. When the server processes Compensate Increment, it checks to see if any Increment messages with that ID have already been processed. If so, the server decrements the value to compensate. If not it leaves the value unchanged. Then in both of the previous cases, it saves the ID so that any future messages with that ID will be ignored.
The literature also refers to each step in a Distributed Saga as a transaction, but I’ve called them actions here to avoid any confusion with other methods of concurrency control.
About the author
Seth Archer Brown is currently writing a free book called Computer Networks From Scratch. If you like what you saw here, you’ll find similar content in the book.
Computer Networks From Scratch is a tour of the inner workings of the biggest computer network of them all–the internet. It starts completely from scratch (assuming no network knowledge at all) with an example system that allows users to send messages back and forth using marbles and plastic tubing instead of electrical signals and wires. Then it builds up to something resembling a state-of-the-art computer network from the early 60s.
The book is a work in progress, but by the end of the book it will provide an overview of the internet as it works today, as well as what’s on the horizon.
Very interesting base problem and read! Really appreciate the connection to a modern scenario as well, thanks!
I admit to not reading the entire article, but I’ll still submit my solution.
Alice to Bob (one and only message sent by courier):
Hi Bob. Let’s attack tomorrow at noon. I’ll be ready and waiting for you to fire off a red and green flare at noon tomorrow if you agree. Upon seeing your flares, I will fire off a blue flare indicating that I’m attacking. (Alice knows Bob would never normally fire off red and green flares, nor would Alice fire blue).
This is penguinpie’s solution with a 3 flare gun fast acknowledgement. This ought to be fast enough.
This was a really nice read!
I think maybe the property we would like to have in the compensating action is the absorbing element, something like the zero for the multiplication, regardless of it being used once or many times the result is the same and it is commutative and idempotent.
The concept may be too mathematical but the analogy with the multiplication could be a good proxy.
I’ve subscribe to the newsletter after reading this!
Place a light rope on each messenger. one end contains a confirmation token around the messenger’s waist and a piece of paper, the other end is tied to a horse. When messenger arrives -he signs the paper with a predetermined codeword and unties the rope. A horse on the other end of the rope is whipped into running at a time it takes to cross the valley, successfully or unsuccessfully dragging the token and signed codeword BACK to the original side, . New messengers arriving, indicate to receiver that previous rope token paper was not received. when new messengers stop arriving, receiver knows last rope made it through. SUCCESS = Original messengers stay on receiver side with attack message, receipt of ropes with attached tokens and signatures. No new messengers sent/arrive. Attack = 100%
@ELC @unixrab Welcome to the forums guys. Interesting responses. How long is this rope? jk